Recursive functions in Power Query are not very popular, but sometimes very helpful when in need. In this post, I’ll explain what a recursive function is, how it works, and explain it through a famous recursive example of Fibonacci Sequence.
Fibonacci Sequence
Fibonacci sequence is one of the fundamental recursive operations in math, below are a few numbers from this sequenece:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34…
As you can see, the numbers above, don’t follow a normal order. Each number is the sum of the two numbers before it:
34= 21+13
21= 13+8
13= 8+5
…
Although I love math, I am not that advanced to explain to you the benefits of this sequence. Here is the Wikipedia page with more info about the Fibonacci Sequence if you wish to read more. My goal here is not to explain to you what this sequence is, but to use to teach you Power Query recursive function.
Recursive Function
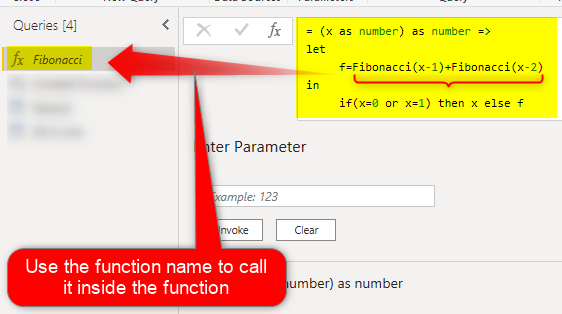
Recursive function is the function that call itself to produce a result. in the above definition of the Fibonacci Sequence. the numbers are called as Fx like below:
F(0)=0
F(1)=1
F(2)=1
F(3)=2
F(4)=3
F(5)=5
F(6)=8
F(7)=13
F(8)=21
F(9)=34
…
When you look at the calculation, each Fx is the sum up of the two Fx before, so the calculation is:
F(x)=F(x-1)+F(x-2)
This means that if I want to calculate the value of F(9), I first need to calculate the value of F(8), and F(7), but then for those I need calculate F(6), and F(5) too, and etc.
The function call with the number X, will cause calling the function again with X-1, and X-2, and that will cause it again for the rest of the loop until it hits 1 or 0. The F(1)=1, and the F(0)=0.
Power Query Function
Writing a Power Query recursive function is very simple. In fact, you don’t even need to do anything except the fact that you need to create a function, and use the function inside itself, like below;
Start with a Blank Query;
Rename the Query to Fibonacci.
And then write the function code below;
= (x as number) as number =>
let
f=Fibonacci(x-1)+Fibonacci(x-2)
in
if(x=0 or x=1) then x else fAs you can see, I have used the function name inside the function itself, saying that if the input parameter is not 1 or zero, then return the same function with x-1 and x-2;
For understanding the code above, first, you need to understand how custom functions work in Power BI. I explained that concept in another article with full details about input parameters, and other blocks of the function’s structure. I recommend you to read that article to understand the structure more.
As you can see, the only thing I needed in the above expression, was to use the function name (or let’s say the Power Query query name) inside the function itself. This only works if your function is defined as a query itself. for Inline functions, you need to use another approach, which I’ll explain later in this article.
Using the Function
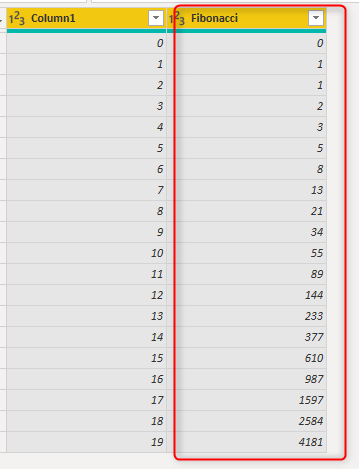
Now if I want to test the function to see how it works, I can call it for a series of numbers, with using the Add Column, Invoke Custom Function;
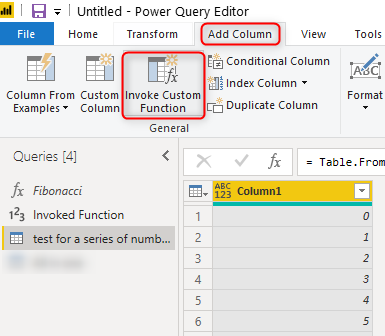
Now the custom function query would be the name of the function, and the input would be the column that includes the numbers;
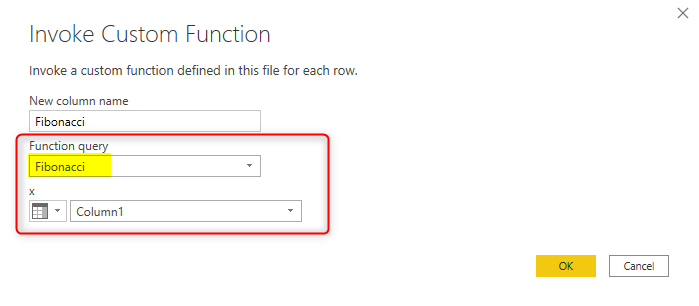
The result simply is the Fibonacci Sequence value for each number:
Consider Exit for the Function
Writing a custom function that works recursive is simple, you just use the function name and that’s all, but having an Exit criteria for that function is necessary. without the exit criteria, your function falls into an endless loop. here is an example of such function (don’t invoke the function below, it might cause you closing your Power BI Desktop 😉)
= (x as number) as number =>
let
f=Fibonacci(x-1)+Fibonacci(x-2)
in
fThe above function falls into an endless loop, for calculating each number, you calculate the two numbers before, and this never ends!
If you compare the above with the Fibonacci function we have created previously, you’ll see that there is an IF statement in that which defines when the recursive loop has to finish:
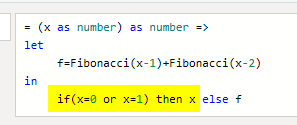
A recursive function without Exit, causes an endless loop, and cannot be used.
Inline Power Query Recursive Function
If your function is defined as a query, then creating a recursive structure in it, means just calling the function’s name. However, if the function is not a separate query itself, then the process is different.
Below is an example of a function that created only inside the below query. This function does not exists as a separate query itself.
let
Source = List.Numbers(0,20),
#'Converted to Table' = Table.FromList(Source, Splitter.SplitByNothing(), null, null, ExtraValues.Error),
F= (x as number) as number =>
let
f=F(x-1)+F(x-2)
in
if(x=0 or x=1) then x else f,
#'Invoked Custom Function' = Table.AddColumn(#'Converted to Table', 'Fibonacci', each F([Column1]))
in
#'Invoked Custom Function'The function above is highlighted inline the main query;
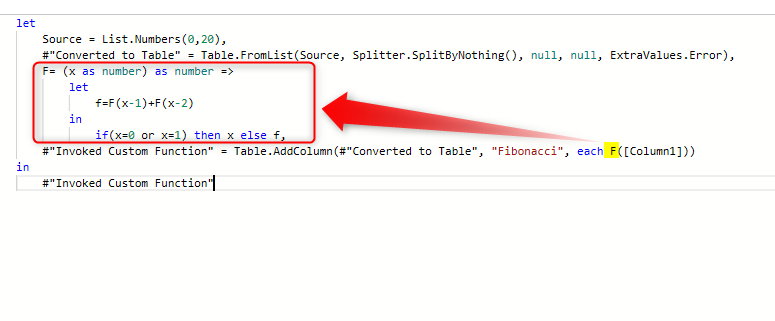
The function is defined inside the query, and it is called using the function name, which in this case is F.
The result, however is error;
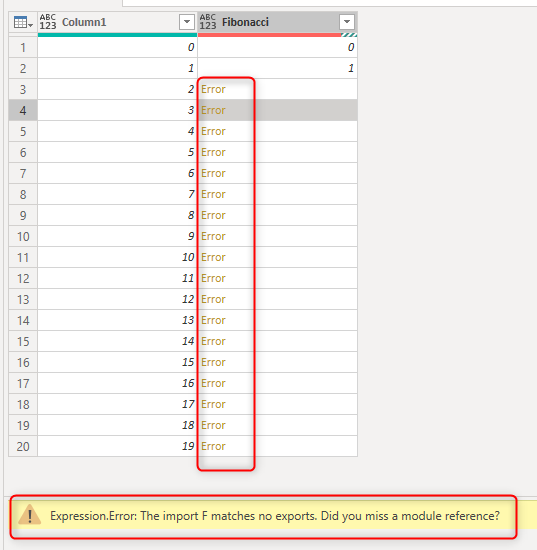
Because there is no query called F, the expression above fails. For the inline Power Query functions, in order to call the function itself, you have to use the character @ before the function name. This character act as the function reference. Below is a code that works correctly;
let
Source = List.Numbers(0,20),
#'Converted to Table' = Table.FromList(Source, Splitter.SplitByNothing(), null, null, ExtraValues.Error),
F= (x as number) as number =>
let
f=@F(x-1)+@F(x-2)
in
if(x=0 or x=1) then x else f,
#'Invoked Custom Function' = Table.AddColumn(#'Converted to Table', 'Fibonacci', each F([Column1]))
in
#'Invoked Custom Function'The two function calls that are inside the inline function are prefixed with @. the function call outside is just normal without @.
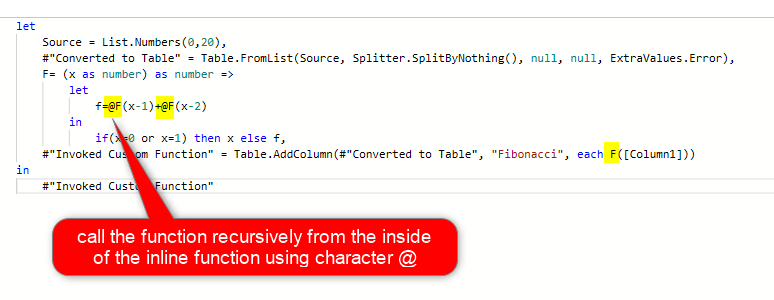
The character @ is called the inclusive-identifier-reference. This can be used for accessing the environment that includes the identifier being initialized.
The result using the above code is working correctly as below;
Summary
Recursive functions, although not very common, but are useful in some instances in Power Query and Power BI. In this article, you learned that you can create a recursive function by calling the function name (if it is not an inline function), or using the inclusive identifier reference (character @) if the function is inline. In both cases make sure that your function always have an Exit criteria and doesn’t fall into an endless loop.
Download Sample Power BI File
Download the sample Power BI report here:
Video
Reza is author of more than 14 books on Microsoft Business Intelligence, most of these books are published under Power BI category. Among these are books such as Power BI DAX Simplified, Pro Power BI Architecture, Power BI from Rookie to Rock Star, Power Query books series, Row-Level Security in Power BI and etc.
He is an International Speaker in Microsoft Ignite, Microsoft Business Applications Summit, Data Insight Summit, PASS Summit, SQL Saturday and SQL user groups. And He is a Microsoft Certified Trainer.
Reza’s passion is to help you find the best data solution, he is Data enthusiast.
His articles on different aspects of technologies, especially on MS BI, can be found on his blog: https://radacad.com/blog.