Time series Series with Power BI- Arima Model-Part 11

In the last post, I have explained the d value for model ARIMA (p,d,q).

In this post, I am going to show how to identify the p and q values as below.

one of the main difference between exponential smoothing and Arima is that Arima considers the correlation of a value at a time with other values which we call autocorrelation.

to see this autocorrelation we need two charts:acf and pacf. but what they are and how they are related to p and q value

acf value or q

acf or (Autocorrelation chart). tries to find a correlation between a value and it successive. there may be a correlation between the value in time t and time t-1. however, these the value in time t may be also related to time 1,2 or any other time.

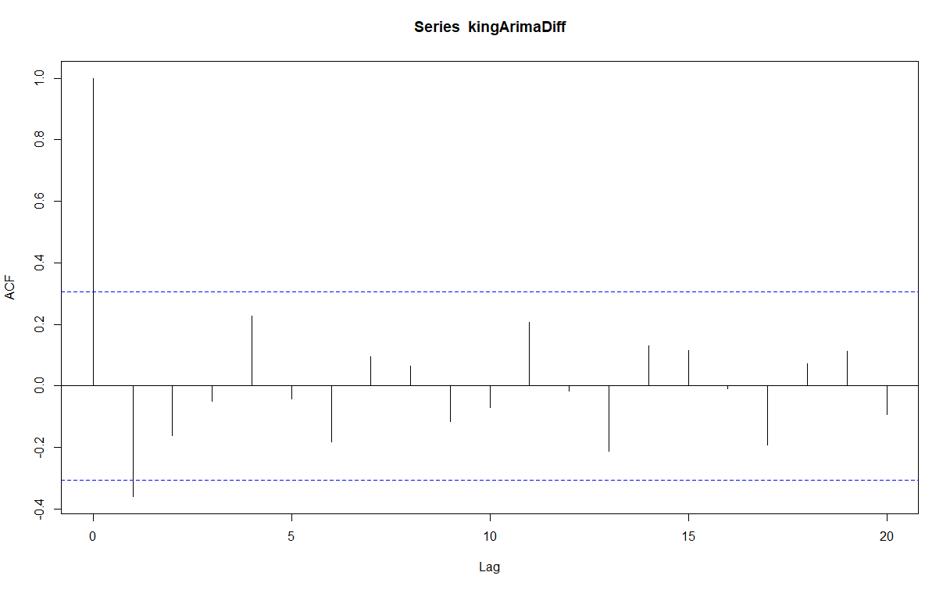
I create a plot for acf and for kings death age.

acf(kingArimaDiff,lag.max = 20)

what we have is below chart, this chart shows how the value in a different time from 1 to 20 is correlated to current time values. for instance for current time the correlation is 1 with itself. in time 2 it is a bit high and we can say there is a correlation between values in time 1 and time 2., however, we could not see any other correlation after time 2.  so the value for q will be 1 as, after time one, we have no correlation.

pacf Value or p

now, we are going to see what is pacf value. pacf is partial autocorrelation values, that means we just purely consider the autocorrelation between time t and time t-1 with removing other correlation with t1,t2 or any other time, we just consider the correlation between time 1 and time 2.

now, we are going to see this partial correlation

pacf(kingArimaDiff,lag.max = 20)

above picture shows there is a correlation between time 1 and time 2 and 3 after time 3 there is no correlation. so p=3.

in other words we able to model our ARIMA model as

ARIMA(p=3,d=1,q=1) however, we able to choose we also below models

ARIMA(p=3,d=1,q=0)

ARIMA(p=0,d=1,q=1)

there is a rule that we better to choose a model with lower value so the final ARIMA model would be :ARIMA(0,1,1)

The above times series does not have any seasonality. in the next post, I will show you how to create an ARIMA model that support seasonality. Then I will explain how to forecast data.

http://a-little-book-of-r-for-time-series.readthedocs.io/en/latest/src/timeseries.html

Leila Etaati

Trainer, Consultant, Mentor

Leila is the first Microsoft AI MVP in New Zealand and Australia, She has Ph.D. in Information System from the University Of Auckland. She is the Co-director and data scientist in RADACAD Company with more than 100 clients in around the world. She is the co-organizer of Microsoft Business Intelligence and Power BI Use group (meetup) in Auckland with more than 1200 members, She is the co-organizer of three main conferences in Auckland: SQL Saturday Auckland (2015 till now) with more than 400 registrations, Difinity (2017 till now) with more than 200 registrations and Global AI Bootcamp 2018. She is a Data Scientist, BI Consultant, Trainer, and Speaker. She is a well-known International Speakers to many conferences such as Microsoft ignite, SQL pass, Data Platform Summit, SQL Saturday, Power BI world Tour and so forth in Europe, USA, Asia, Australia, and New Zealand. She has over ten years’ experience working with databases and software systems. She was involved in many large-scale projects for big-sized companies. She also AI and Data Platform Microsoft MVP. Leila is an active Technical Microsoft AI blogger for RADACAD.